第四届西安几何拓扑会议
2024.6.29-30,西安交通大学

============================================================================================
第三届西安几何拓扑会议
2022.5.14-15,腾讯会议
http://math.xjtu.edu.cn/info/1089/11281.htm


=======================================================================================================================================
第二届西安几何拓扑会议
2020.9.19-20,西安交通大学

日程 http://math.xjtu.edu.cn/info/1089/9948.htm
照片 http://math.xjtu.edu.cn/info/1213/9967.htm
=====================================================================================================================================
西安几何拓扑会议
2019.9.20-22,西安交通大学 数学楼2-1会议室

![]()

![]()





















2019.9.23
============================================================================================================================
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
============================================================================================================================
曲面映射类群相关课题研讨班
2015.8.16-19,西安交通大学(主楼A座103)
















日程安排:8.16主题报告、8.17-19系列短课
|
8.16周日 |
报告人 |
主持人 |
|
8:30-8:50 |
开幕式 |
|
|
8:50-9:40 |
李韬 |
高红铸 |
|
9:40-10:10 |
照相 |
|
|
10:10-11:00 |
杜晓明 |
包志强 |
|
11:10-12:00 |
叶圣奎 |
|
|
12:00-14:00 |
午饭 |
|
|
14:00-14:50 |
邱瑞锋 |
杨志青 |
|
14:50-15:10 |
茶歇 |
|
|
15:10-16:00 |
邹燕清 |
程志云 |
|
16:10-17:00 |
余斌 |
|
|
|
8.17周一 |
8.18周二 |
8.19周三 |
|
8:30-9:30 |
张影 |
张影 |
杨文元 |
|
9:30-9:50 |
茶歇 |
||
|
9:50-10:50 |
张影 |
张影 |
杨文元 |
|
11:00-12:00 |
马继明 |
杨文元 |
李友林 |
|
12:00-14:00 |
午饭 |
||
|
14:00-15:00 |
马继明 |
杨文元 |
李友林 |
|
15:00-15:20 |
茶歇 |
||
|
15:20-16:20 |
王家军 |
叶圣奎 |
杜晓明 |
|
16:30-17:30 |
王家军 |
叶圣奎 |
杜晓明 |
8.16日报告题目、摘要:
1. 李韬:Tunnel numbers and satellite knots
2. 杜晓明:映射类群的有限阶生成元集du-2015xjtu.pdf
摘要:本报告介绍映射类群的生成元集的刻画方式,其中包括用二阶和三阶元来生成映射类群等方面的工作。
3. 叶圣奎:Zero-in-the-spectrum Conjecture and Homology equivalences
Abstract: The zero-in-the-spectrum conjecture asks that for a closed aspherical manifold, whether there is always a nonzero L^2 homology group. Farber-Weinberger construct some (counter-)examples for nonaspherical manifolds. Theses examples were generalized by Higson-Roe-Schick. In this talk, we will propose a general construction of these examples, using the concept of group-dense rings. Such a general construction has further applications to Quillen's plus construction, homology spheres and one-sided cobordims, ect.
4. 邱瑞锋:On distance of Heegaard splitting
5. 邹燕清:Stability of the canonical Heegaard splitting of a mapping torus
Abstract: The mapping tori is mostly studied in 3-manifolds, especially for those ones over pseudo-Anosov maps. Although mapping tori are just quotient space of surface I-bundles over some gluing maps, the undetermined property of pseudo-Anosov maps make mapping tori flexible and complicated. In this talk, we will focus on the canonical Heegaard splitting of a mapping torus. With tools developed in curve complex, we proved that if the translation distance of a pseudo-Anosov map is larger than 8, then the canonical Heegaard splitting is unstabilized. This result is a more refined one proved by Souto etc.
6. 余斌:Smale solenoid attractors in 3-manifolds Solenoidsmale.pptx
8.17-19日短课内容:
1. 张 影:Geodesic Laminations on Surfaces
2. 马继明:Scissors congruence
3. 王家军:Distance in the complex of curves
4. 杨文元:Rotating families with applications to mapping class groups.
Abstract: This will be a series of talks to explain the ingredients of the theory of rotating families. This theory allows Dahmani-Guirardel-Osin to show that there are lots of free, purely pseudo-Anosov, normal subgroups of mapping class groups. This resolved two long-standing open problems.
Reference: F. Dahmani, V. Guirardel, D. Osin: Hyperbolically embedded subgroups and rotating families in groups acting on hyperbolic spaces, arXiv:1111.7048
5. 叶圣奎:L2-Invariants
6. 李友林:Lefschetz fibration and mapping class groups
7. 杜晓明:Dehn-Nielsen定理
与会者:
|
姓名 |
单位 |
|
包志强 |
北京大学 |
|
陈海苗 |
北京工商大学 |
|
陈智 |
合肥工业大学 |
|
程志云 |
北京师范大学 |
|
邓嘉龙 |
首都师范大学 |
|
杜晓明 |
华南理工大学 |
|
高红铸 |
北京师范大学 |
|
李韬 |
|
|
李友林 |
上海交通大学 |
|
马继明 |
复旦大学 |
|
邱瑞锋 |
华东师范大学 |
|
孙磊 |
东北林业大学 |
|
王晁 |
中国科技大学 |
|
王家军 |
北京大学 |
|
文诗云 |
首都师范大学 |
|
徐勐戬 |
北京师范大学 |
|
杨文元 |
北京大学 |
|
杨志青 |
大连理工大学 |
|
叶圣奎 |
西交利物浦大学 |
|
余斌 |
同济大学 |
|
张恺 |
大连理工大学 |
|
张强 |
西安交通大学 |
|
张一木 |
吉林大学 |
|
张影 |
苏州大学 |
|
邹燕清 |
大连民族大学 |
联系人:张强 Email: zhangq.math@mail.xjtu.edu.cn
交通信息:
1. 西安咸阳国际机场——馨乐庭兴庆宫公寓(地址:兴庆南路交大电脑城对面)
l 出租车:约60分钟,150元
l 机场巴士西安火车站线(每30分钟一班)到终点陇海大酒店(约60分钟,26元),然后出租车至馨乐庭(约15分钟,15元)
l 机场巴士建国线(每60分钟一班)到终点建国饭店(约60分钟,26元),然后出租车至馨乐庭(约5分钟,10元)
2. 西安北站——馨乐庭兴庆宫公寓(地址:兴庆南路交大电脑城对面)
l 西安北站出检票口直接乘地铁2号线到永宁门(11站、30分钟)出D2口,换乘出租车至馨乐庭(约10分钟,12元)或换乘公交800或402到交大电脑城(15分钟)下车步行
l 出租车:约50分钟,60元
3. 西安站——馨乐庭兴庆宫公寓(地址:兴庆南路交大电脑城对面)
l 出租车:约15分钟,15元
l 出火车站直行
4. 住交大招待所的老师和同学,请先到馨乐庭兴庆宫公寓报到,然后由我们带您去交大招待所入住。
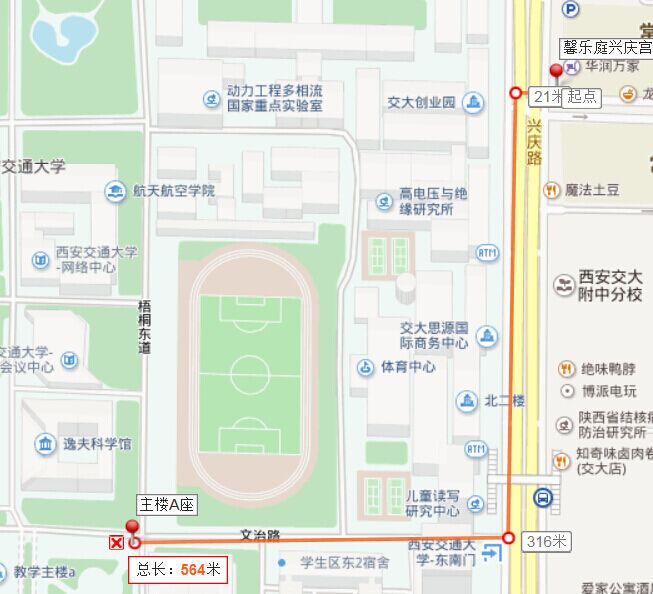
馨乐庭兴庆宫公寓至会场(主楼A座103)路线图:
最后更新于2015.8.26.




