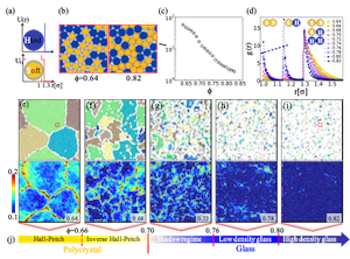
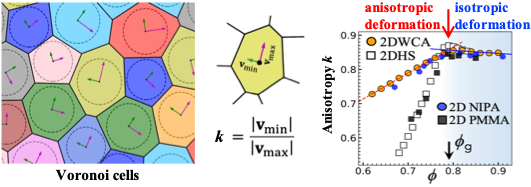
[5] Huijun Zhang*, Qi Zhang, Feng Liu, and Yilong Han*, Anisotropic–Isotropic Transition of Cages at the Glass Transition. Physical Review Letters 132, 078201 (2024)  (中科院一区,IF = 8.6)
(中科院一区,IF = 8.6)
玻璃转变(从流动性液体到刚性固体)的结构变化是凝聚态物理领域的研究难题。我们用Voronoi表征局部笼结构(cage),定义各项异性参数k,发现cage的演化:液体->各项异性,玻璃态->各向同性,其转变点对应MCT动力学转变点。此参数k还可解释自由体积理论和液体与玻璃中的结构幂律v ~ q1-d。
[4] Huijun Zhang*, Chengjie Luo, Zhongyu Zheng*, and Yilong Han*, Effects of size ratio on particle packing in binary glasses. Acta Materialia 246, 118700 (2023)  (中科院一区,IF = 9.4)
(中科院一区,IF = 9.4)
当调节玻璃态组分时,存在分数幂律v ~ q1-d, d < D [Nat. Mater. 8, 30 (2009)],但机理不明。我们调节多种金属玻璃和硬球玻璃系统,观察到分数幂律幂指数d与大小球尺寸比λ直接相关,且玻璃态结构在λ < 1.2时不稳定(d > D),而λ > 1.2时稳定(d < D),多种结构量也在λ = 1.2处发生转变。

[3] Huijun Zhang*, Feng Liu, Goran Ungar, Zhongyu Zheng, Qingping Sun, and Yilong Han*, A Regime beyond the Hall-Petch and Inverse-Hall-Petch Regimes in Ultrafine-Grained Solids. Communications Physics 2022, 5, 329 (2022).  (中科院一区,IF = 6.497)
(中科院一区,IF = 6.497)
多晶材料强度随晶粒尺寸下降会先增强后下降,谓之Hall-Petch强化和inverse Hall-Petch软化现象[Science 301, 1357 (2003); Science 355, 1292 (2017)]。软化现象之后是什么情况并不清楚,原因是超细纳米晶粒不稳定,难以获取。我们发表于2018PRX的工作,可以将晶粒尺寸连续下降至非晶态。观察到Hall-Petch和inverse Hall-Petch现象之后一个新的符合幂律关系的增强区域,给出了晶体/非晶态复合结构材料强度与晶粒尺寸关系的全貌图。

[2] Huijun Zhang, Kaiyao Qiao, and Yilong Han*, power laws in pressure-induced structural change of glasses. Nature Communications 11, 2005 (2020)  (中科院一区,IF = 16.60)
(中科院一区,IF = 16.60)
压缩金属玻璃观察到分数幂律v ~ q1-d, d < D空间维度[Phys. Rev. Lett. 112, 185502 (2014); Proc. Natl. Acad. Sci. 113, 1714 (2016)],但机理不明。我们模拟压缩三种玻璃系统,澄清分数幂律(d < D)仅存在于组元硬度不同的玻璃系统(如软硬混合系统),且与组元可压缩量直接相关。此幂律关系也可用来判断晶体-非晶转变。

[1] Huijun Zhang and Yilong Han*, Compression-induced polycrystal-glass transition in binary crystals,Physical Review X, 8, 041023 (2018)  (中科院一区,IF = 14.42)
(中科院一区,IF = 14.42)
多晶随着晶粒尺寸下降必然会进入非晶态,但多晶-非晶的边界在哪里还未见研究。我们模拟压缩二元合金,观察到随晶粒尺寸连续下降,结构、动力学、力学、热力学量在特定晶粒尺寸发生明显转变,揭示了多晶-非晶的转变(边界)。