Last updated October 16, 2014
SMAT - MATLAB toolbox for parameter identification of consitutive models
Overview (see manual 
):
SMAT is a MATLAB toolbox containing the following features
- Identify the material parameters based on optimisation method
- Create publication ready plots
- Writting scripts to process many data sets
Author:
The SMAT toolbox is developed and maintained by Dr. Shun-lai ZANG
Dr. Shun-lai ZANG
School of Mechanical Engineering
Xi'an Jiaotong University
No.28, Xianning West Road, Xi'an, Shaanxi, 710049, P.R. China
Website:
All SMAT releases, development news, FAQs can be found on the SMAT hompage [[http://shawn.gr.xjtu.edu.cn/]]
Credits:
The toolbox is referred upon the following great software packages:
*SiDoLo - P. Pilvin [[http://web.univ-ubs.fr/limatb/]]
*MTEX - Dr. Ralf Hielscher
[[http://www-user.tu-chemnitz.de/~rahi]]
Copyright (C) 2010-2014 Shun-lai Zang:
This software has been registered as the software patent (No. 2013SR038190).
Flow chart and Screenshot:
Fig.1 The flow chart of SMAT Matlab toolbox. Fig.2 The screenshot of SMAT Matlab toolbox.
Applications:
@Measurement of the Bauschinger behavior of sheet metals by three-point bending springback test with pre-strained strips. For a pre-strained sheet, the innear material experiences tension-compression deformation after the subsequent three-point bending. Therefore the Bauschinger behavior has an influence on the bending moment before springback. Since the springback is mainly related to the elastic properties of the material and the bending moment before unloading, the Bauschinger behavior of metallic sheet can be determined from the springback of three-point bending test with pre-strained sheet. (ANK-E(ep)-Opt. means the material parameters are determined from the new approach.) |
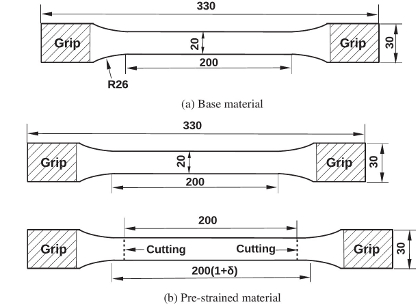
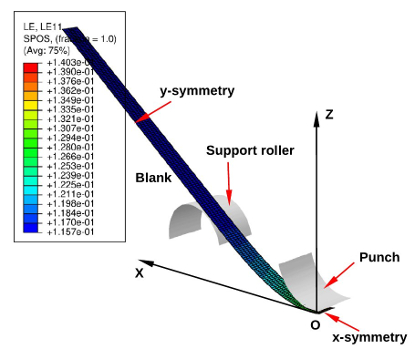Fig.3 Dimensions of three-point bending test with prescribed tension. Fig.4 The finite element simulation of three-point bending test.
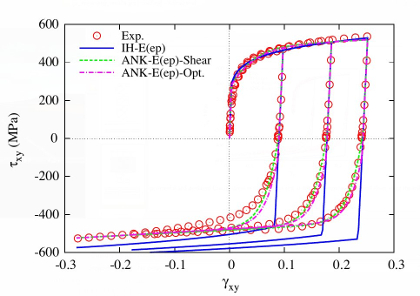
Fig.5 Samples after the three-point bending. Fig.6 The predicted Cauchy stress in simple shear test.
