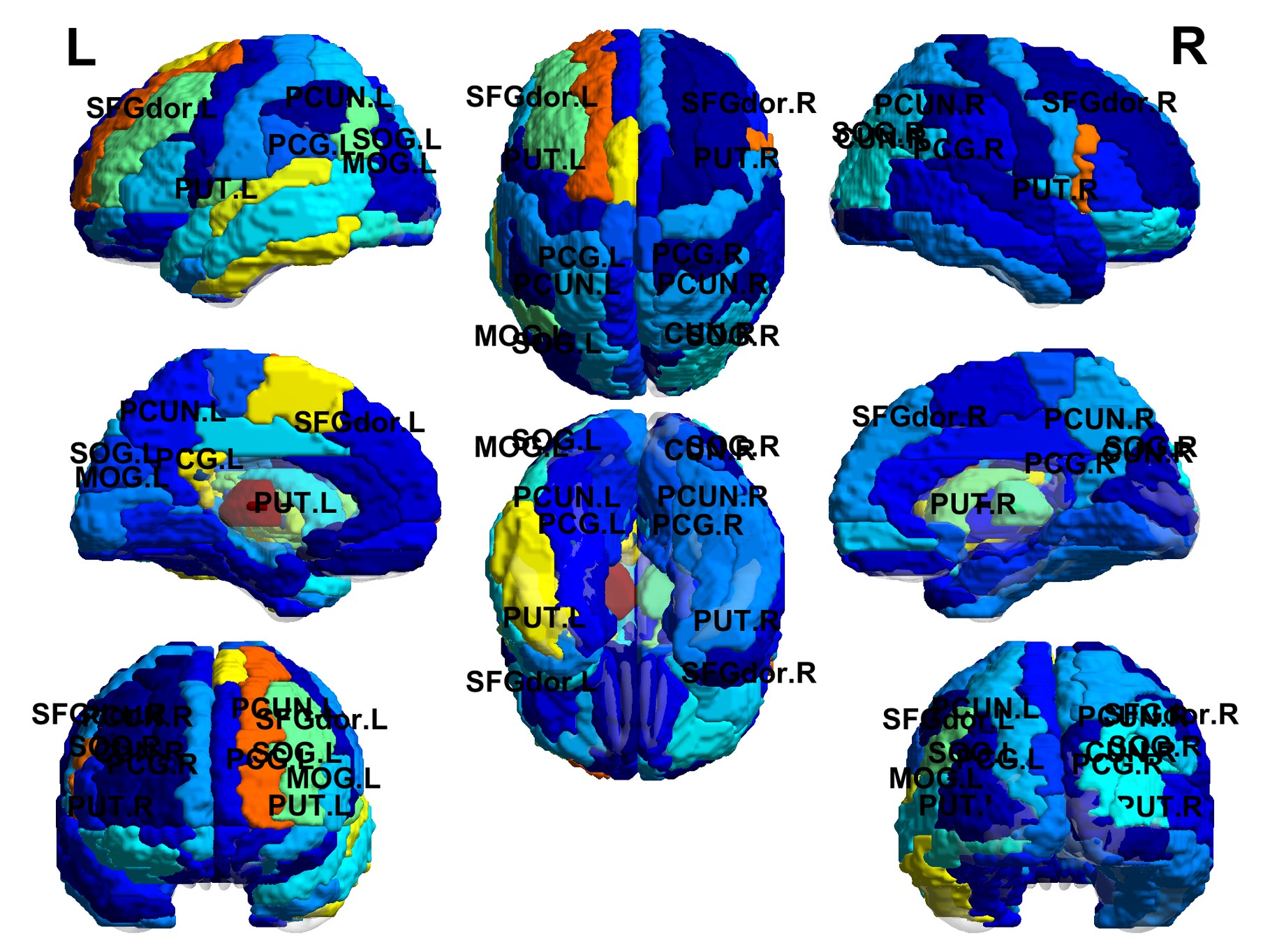
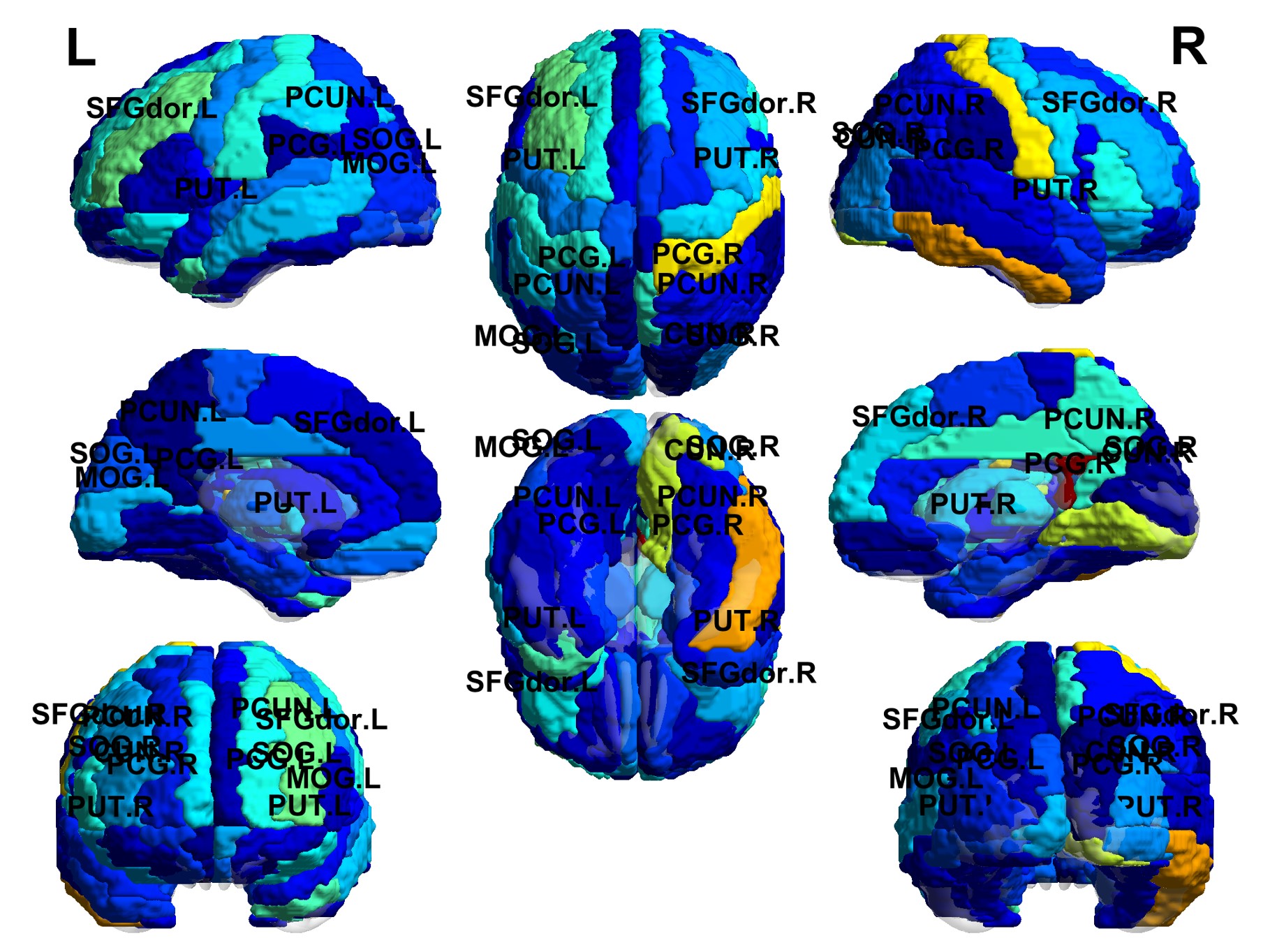
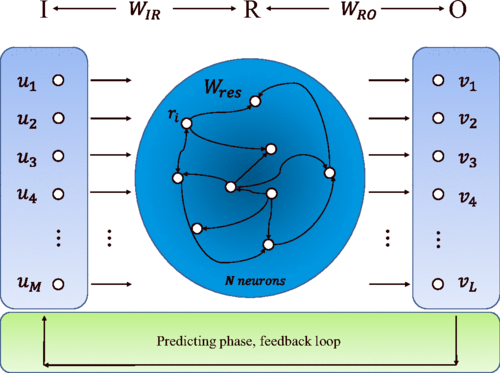
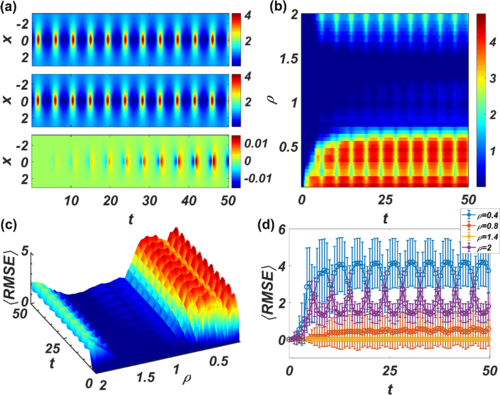
新皮层中如何通过重复的标准局部环路架构产生功能模块化？我们通过聚焦工作记忆这一核心认知功能来探讨这个问题。我们提出了“空间分叉”的机制，并展示其显著特征为“临界减速”的空间局部化，导致工作记忆过程中皮层层级中神经元时间常数呈倒V型分布。该现象在基于小鼠和猴子连接组的大规模模型中得到验证，提供了一个实验可测试的预测，并用以评估工作记忆表征是否模块化。多个空间分叉可以解释不同活动模式的出现，可能用于不同的认知功能。本研究表明，分布式心理表征与功能特异性是兼容的，这源于皮层宏观神经生物学特性的梯度，提出了理解大脑模块化组织的一般原则。

最新的连接组学和神经生理学进展使探究全脑认知和行为机制成为可能。我们开发了一个多区域小鼠大脑的大规模模型，用于研究工作记忆这一重要认知功能，即大脑在没有感觉输入的情况下内部持有和处理信息的能力。该模型基于介观连接组数据构建，包含皮层间连接，并具有测量的表达小清蛋白的中间神经元密度的宏观梯度。我们发现，工作记忆编码是分布式的，但表现出模块化特性；记忆表征的空间模式由长距离、细胞类型特异性的目标和细胞类别密度决定。细胞类型特异性的图测量预测了活动模式和记忆维持的核心子网络。模型展示了众多吸引子状态，即自我维持的内部状态（每个状态涉及不同的区域子集）。本研究提供了一个解释认知过程中大规模脑活动记录的框架，同时强调了细胞类型特异性连接组学的必要性。

全球范围内，神经和精神疾病（如抑郁症、焦虑症、精神分裂症和阿尔茨海默病等）患病率很高，影响数亿人，造成巨大的社会和经济负担。许多疾病的诊断仍依赖于主观临床评估，缺乏客观生物标志物。因此，通过研究找到更有效的预防和治疗方法，对应对未来的健康挑战至关重要。目前，针对这些疾病的研究主要集中在结构或功能网络连接的变化上，揭示了不同脑区之间连接强度和模式的变化。然而，这些研究未能充分测量特定脑区的性质变化，限制了对疾病机制的全面理解。在这方面，基于结构连接的全脑计算模型可以高度解释每个脑区在健康和疾病状态下的动态特性。这种方法为理解脑功能原理和脑疾病的病理机制提供了新的见解。其中，Landau-Stuart振荡器网络模型中的异质性参数有效描述了每个脑区的内在动态特性，有望增强我们对脑功能及相关疾病的理解。然而，当前参数估计技术的精度和可靠性不足，限制了该模型在研究和临床中的实际应用, 我们的研究是首次系统性验证和改进专门针对Landau-Stuart振荡器网络模型的参数估计方法: 参数估计的稳定性提高了38.94%，与实际参数的相关性增加了22.58%，数据特征拟合的准确性提高了82.51%，从而提升了模型的整体效能。

在机器学习应用中，一个常见的难题是缺乏指导选择神经网络超参数的一般原则。专注于一种用于无模型预测非线性动力系统的循环神经网络——储备池计算，我们发现了一个惊人的现象：在神经网络的谱半径中出现了一个区间，使得预测误差最小。在误差与时间及谱半径的三维表示中，这个区间对应于“山谷”底部。这种山谷现象在由非线性偏微分方程描述的各种时空动力系统中都会出现，无论基础库网络的结构和边权分布如何。我们还发现，虽然山谷的位置和大小依赖于待预测系统的具体细节，但对于无向网络，这个区间往往更大。山谷现象有助于设计最优的储备池计算，这在理解这些机器学习系统方面迈出了一小步。

研究和借鉴哺乳动物感认知系统高度发达的能力，有望帮助我们开发适应复杂环境的系统，我们尝试通过电生理信号提取及解码技术相结合，实现这种系统。

从生态系统、气候到经济、社会和基础设施系统等复杂网络系统，都可能出现临界点，即系统完全崩溃的“不可回返点”。理解临界点的动力机制并预测其发生至关重要，但这一任务受到系统高维性的阻碍。我们以复杂的互惠网络作为生态系统的原型，通过降维过程得到一个有效的二维系统，这两个动态变量对应于平均传粉者和植物的丰度。使用59个从真实数据中提取的经验互惠网络，我们展示了二维模型可以在存在随机干扰的情况下准确预测临界点的发生。我们还发现，由于真实网络结构中缺乏足够的随机性，在降维过程中需要加权平均。我们的简化模型可以作为理解和预测现实互惠网络中临界点动力学的范例，保护传粉者，并将这一通用原理扩展到广泛的学科，以解决弹性和可持续性问题。

另一方面，我们利用现实中的传粉者和植物的互惠网络作为原型系统，并考虑生物约束，我们开发了一种生态可行的策略，通过维持某一传粉者种群的丰度在恒定水平来管理/控制临界点，从而消除与临界点相关的迟滞效应。如果条件变化接近临界点，我们描述的管理策略可以防止突然的剧变。此外，如果系统已经越过临界点，我们证明了只要积极管理丰度，系统在合理参数变化下仍可完全恢复，同样由于消除了迟滞效应。这个临界点后的恢复点可以通过一个通用的二维简化模型预测。

储备池计算被用于无模型、基于数据的各种混沌动力系统状态演化预测，目前预测范围约为六个李雅普诺夫时间。是否有可能显著延长预测时间？我们提出了一种方案，将时间依赖但稀疏的数据输入纳入储备池计算，展示了这些稀疏的“更新”实际上可以实现对各种混沌系统的任意长时间预测。基于时间同步理论，我们提供了物理理解。在现实中，相位信息非常重要，例如生态系统中物种数量的波动、电子电路中电压的极性变化，以及某些化学物质浓度的上下波动。我们以经典混沌振荡器和生态学中的混沌食物网系统为例，展示了储备池计算可用于长期预测混沌振荡器的相位，其典型预测范围可以比预测整个变量长几个数量级，并对此提供了物理理解。我们还展示了一个设计良好的储备池计算机器可以可靠地感知一对耦合混沌振荡器之间的相位同步，这对设计并行储备池计算方案以预测大型混沌系统有重要意义。