Randomized Neural Networks Methods

Partial differential equations (PDEs) are indispensable in a multitude of disciplines including science, engineering, biology, and finance. As computer technology has advanced, numerical methods such as finite differences, finite elements, finite volumes, and spectral methods have evolved rapidly, proving highly effective in applications ranging from weather forecasting to aircraft design and reservoir exploration. Despite their advancements, traditional numerical methods suffer from the "curse of dimensionality" when applied to high-dimensional problems. For example, solving a 20-dimensional Poisson equation using the linear finite element method would require approximately 1040 degrees of freedom to maintain an error magnitude of 10-2, illustrating the limitations of traditional approaches in tackling high-dimensional problems. Moreover, these methods also face significant challenges in solving two-dimensional and three-dimensional PDEs. These methods often struggle with complex domain meshing, while time-iteration schemes can lead to instability and error accumulation, reducing computational efficiency. The substantial computational demand for high-precision and high-resolution simulations makes these traditional methods less suitable for contemporary needs like digital twins, data assimilation, big data integration, and intelligent design.
 

In recent years, a variety of methods based on artificial neural networks have emerged to solve PDEs, showing promise in overcoming some of these challenges. These innovative approaches deserve significant attention and require thorough exploration and research to address the challenges previously mentioned. However, despite their potential, neural network methods based on optimization training often suffer from insufficient accuracy, slow training speeds, and uncontrollable errors due to the lack of efficient optimization algorithms.
 

To leverage the strengths of both traditional and neural network approaches while minimizing their limitations, we explore the use of randomized neural network methods for solving PDEs. This strategy employs the powerful approximation capabilities of neural networks to circumvent the limitations of classical numerical methods, aiming to enhance accuracy and training efficiency. Randomized Neural Networks (RNNs) are a variety of neural networks in which the hidden-layer parameters are fixed to randomly assigned values, and the output-layer parameters are obtained by solving a linear system through least squares. This improves the efficiency without degrading the accuracy of the neural network. 

 

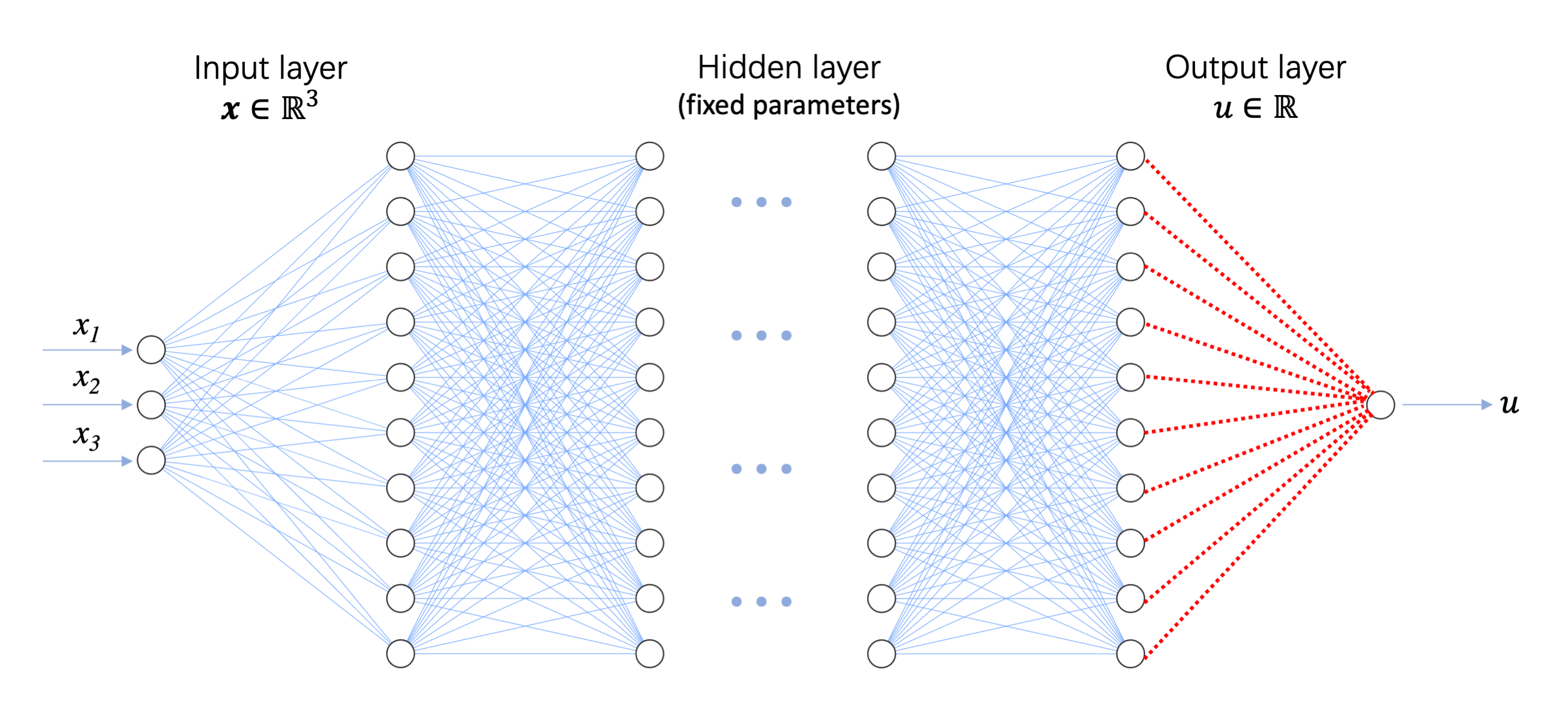
Randomized Neural Network: the solid blue line represents the parameters of the neural network that are
randomly initialized and fixed thereafter, while the dotted red line refers to the adjustable parameters. 

 

In [16], we proposed a new approach for solving partial differential equations (PDEs) based on randomized neural networks and the Petrov-Galerkin method, which we call the RNN-PG methods. This method uses randomized neural networks to approximate unknown functions and allows for a flexible choice of test functions, such as finite element basis functions, Legendre or Chebyshev polynomials, or neural networks. We apply the RNN-PG methods to various problems, including Poisson problems with primal or mixed formulations, and time-dependent problems with a space-time approach. This paper is adapted from the work originally posted on arXiv.com by the same authors (arXiv:2201.12995, Jan 31, 2022). The new ingredients include non-linear PDEs such as Burger’s equation and a numerical example of a high-dimensional heat equation. Numerical experiments show that the RNN-PG methods can achieve high accuracy with a small number of degrees of freedom. Moreover, RNN-PG has several advantages, such as being mesh-free, handling different boundary conditions easily, solving time-dependent problems efficiently, and solving high-dimensional problems quickly. These results demonstrate the great potential of the RNN-PG methods in the field of numerical methods for PDEs. The RNN-PG methods were developed to solve linear elasticity and Navier-Stokes equations in [17].

 

 

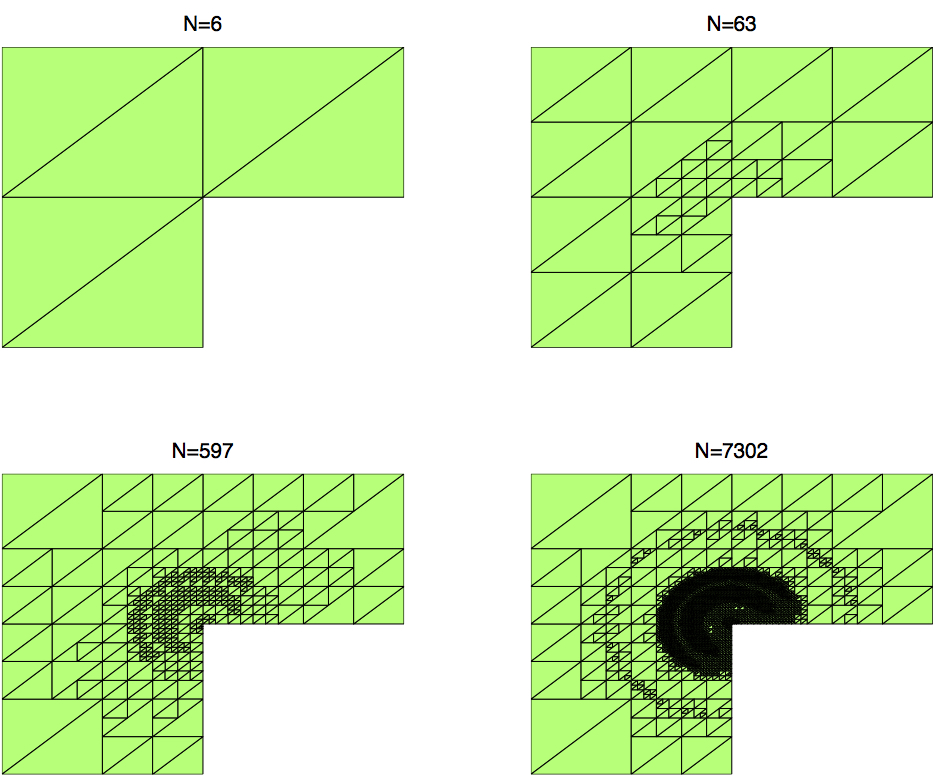
In [18], we combine the idea of the Local RNN (LRNN) and the Discontinuous Galerkin (DG) approach for solving partial differential equations. RNNs are used to approximate the solution on the subdomains, and the DG formulation is used to glue them together. Taking the Poisson problem as a model, we propose three numerical schemes and provide convergence analysis. Then we extend the ideas to time-dependent problems. Taking the heat equation as a model, three space-time LRNN with DG formulations are proposed. Finally, we present numerical tests to demonstrate the performance of the methods developed herein. We evaluate the performance of the proposed methods by comparing them with the finite element method and the conventional DG method. The LRNN-DG methods can achieve higher accuracy with the same degrees of freedom, and can solve time-dependent problems more precisely and efficiently. This indicates that this new approach has great potential for solving partial differential equations. The LRNN-DG methods were developed to solve diffusive-viscous wave equation in [19].

 

 

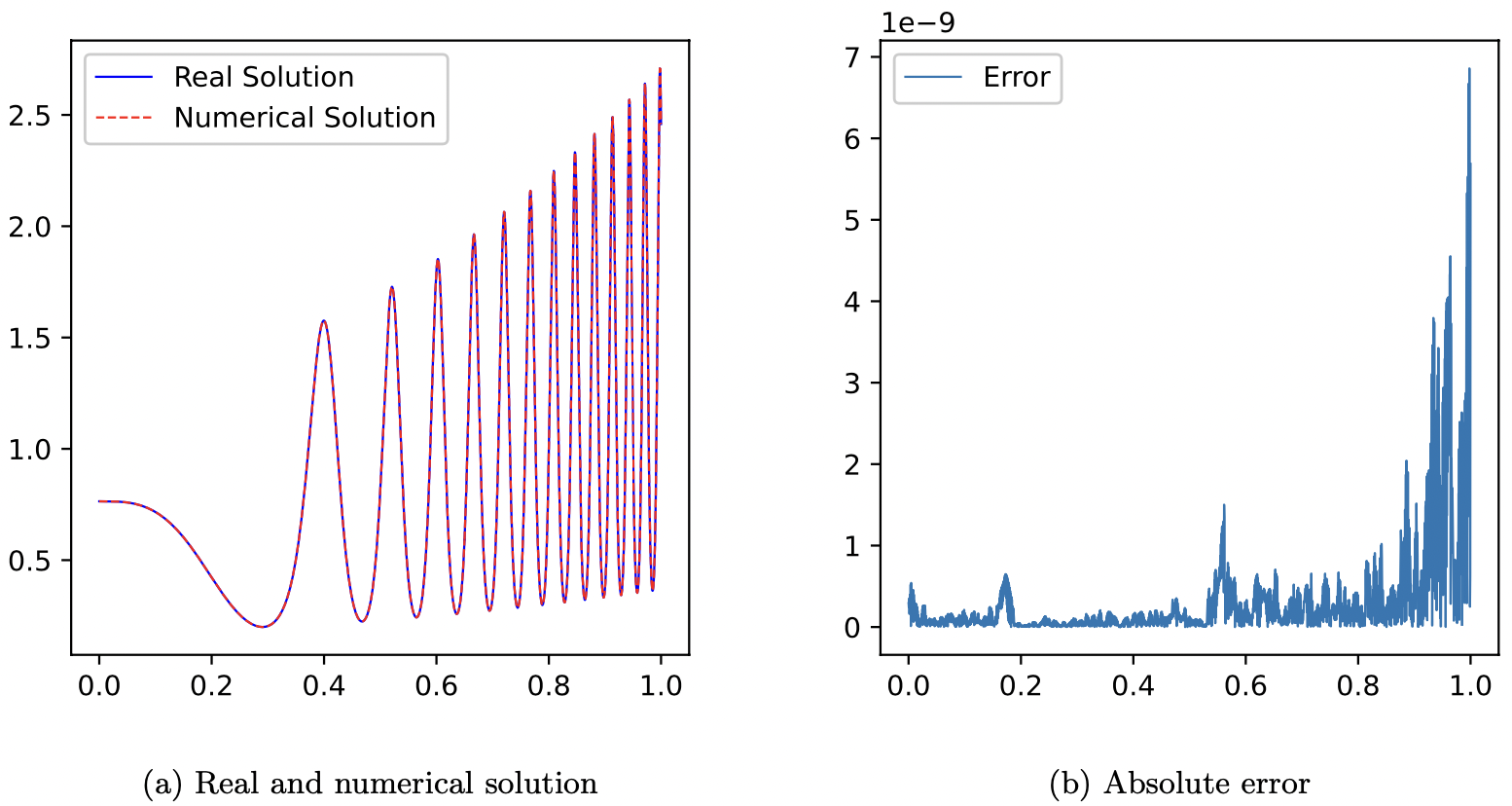
In [20], we explored the use of randomized neural networks (RNNs) for solving obstacle problems, which are elliptic variational inequalities of the first kind that arise in various fields. Obstacle problems can be regarded as free boundary problems, and they are difficult to solve numerically because of their nonsmooth and nonlinear nature. Our first method, RNN with Petrov-Galerkin (RNN-PG), applies RNN to the Petrov-Galerkin variational formulation and solves the resulting linearized subproblems by Picard or Newton iterations. Our second method, RNN with PDE (RNN-PDE), directly solves the partial differential equations (PDEs) associated with the obstacle problems using RNN. We conduct numerical experiments to demonstrate the effectiveness and efficiency of our methods, and show that RNN-PDE outperforms RNN-PG in terms of speed and accuracy.

[16] Yong Shang, Fei Wang* and Jingbo Sun, Randomized Neural Network with Petrov-Galerkin Methods for Solving Linear and Nonlinear Partial Differential Equations, Communications in Nonlinear Science and Numerical Simulation 127, (2023), 107518. (Jan 31, 2022, arXiv:2201.12995)

 

[17] Yong Shang and Fei Wang*, Randomized Neural Networks with Petrov-Galerkin Methods for Solving Linear Elasticity and Navier-Stokes Equations, Journal of Engineering Mechanics 150 (2024), 04024010. (arXiv:2308.03088)

 

[18] Jingbo Sun, Suchuan Dong and Fei Wang*, Local Randomized Neural Networks with Discontinuous Galerkin Methods for Partial Differential Equations, Journal of Computational and Applied Mathematics 445, (2024), 115830. (arXiv:2206.05577).

 

[19] Jingbo Sun and Fei Wang*, Local Randomized Neural Networks with Discontinuous Galerkin Methods for Diffusive-Viscous Wave Equation, Computers and Mathematics with Applications 154, (2024), 128--137. (25 May 2023, arXiv:2305.16060)

 

[20] Fei Wang and Haoning Dang, Randomized Neural Network Methods for Solving Obstacle Problems, Volume on Nonsmooth Problems with Applications in Mechanics，Banach Center Publications, accepted.

Discontinuous Galerkin Methods for Variational Inequalities

Many problems in physical and engineering sciences are modeled by partial differential equations (PDEs). However, various more complex physical processes are described by variational inequalities (VIs). Variational inequalities form an important and very useful class of nonlinear problems arising in diverse application areas of physical, engineering, financial, and management sciences.a

 

Discontinuous Galerkin (DG) Methods for VIs

 
Discontinuous Galerkin (DG) methods have been widely used for solving a variety of mathematical and physical problems due to the advantage of capturing non-smooth or oscillatory solutions effectively and the flexibility in constructing feasible local shape function spaces. Because of their discontinuous nature, DG methods are very suitable for hp-adaptive algorithms. Another advantage is the locality of the discretization, which makes them ideally suited for parallel computing. Moreover, DG methods incorporate non-homogeneous boundary conditions in the weak formulations, which greatly increases the robustness and accuracy of boundary condition implementation. In the past five years, Dr. Wang have worked with Professor Weimin Han (University of Iowa), Professor Xiaoliang Cheng (Zhejiang University) and other collaborators on developing DG methods for solving variational inequalities. Due to inequality form of the problems, the Galerkin orthogonality is lost when DG methods are applied to solve VIs, resulting in substantial difficulty in analyzing DG methods for VIs. Also, the bilinear forms of DG schemes have coercivity only in the finite element spaces, not in the original function space. Therefore, the standard analytical techniques of finite element methods for VIs are not applicable for DG cases. We had to search for a new approach. We studied numerous DG methods for solving elliptic variational inequalities of both the first and second kinds, and established a unified a priori error analysis. We proved that the consistent and stable DG schemes can achieve the optimal convergence order with linear element for various variational inequality problems, such as obstacle problem ([1]) , frictional contact problem ([1]), Signorini problem ([2]), and quasi-static contact problem ([3]). 
 

[1] Fei Wang, Weimin Han and Xiaoliang Cheng, Discontinuous Galerkin Methods for Solving Elliptic Variational Inequalities, SIAM J Numerical Analysis, 48 (2010), 708-733.      

[2] Fei Wang, Weimin Han and Xiaoliang Cheng, Discontinuous Galerkin Methods for Solving Signorini Problem, IMA Journal of Numerical Analysis, 31 (2011), 1754-1772.      

[3] Fei Wang, Weimin Han and Xiaoliang Cheng, Discontinuous Galerkin Methods for Solving the Quasistatic Contact Problem, Numerische Mathematik, 126 (2014), 771-800.

 

Adaptive Finite Element Methods for VIs

 

Compared with uniform mesh, adaptive finite element method can improve precision with smaller memory and less time cost. DG methods are very suitable for hp-adaptive algorithm. Thus, it is a natural choice to study adaptive DG methods for VIs. For the DG schemes of obstacle problems, we derived reliable error estimators of the residual type. The efficiency of the estimators is theoretically explored and numerically confirmed ([4]). It is difficult to develop a posteriori error estimates to variational inequalities due to the inequality feature. The idea was to use Lagrange multiplier to transfer obstacle problem to the associated elliptic PDE, then apply a posteriori error theory of elliptic differential equation to derive reliable error estimators. This idea was extended to give a posteriori error analysis for VIs of the second kind. Moreover, a proof was provided for the efficiency of the error estimators, which was first proved in ([5]). A posteriori error estimates of DG methods for a frictional contact problem was studied, and we proved that the error estimators are reliable and efficient. The following two figures are for one numerical example about adaptive DG for solving obstacle problem. Figure 1 shows the adaptive meshes with hanging nodes, N denoting the number of elements. In Figure 2, the L2 norm and H1 norm errors are given respectively on L2 norm error are 0.097020 and 0.001293, respectively. To achieve the same level of accuracy, with adaptivity, we only need to compute the solution on the mesh $T11$; correspondingly N = 3975, and H1 norm and L2 norm errors being 0.088184 and 0.001134, respectively. Therefore comparing to the uniform refinement, with smaller memory, the adaptive strategy saves lots of computing time. 

 

Figure 1. Adaptive Refined Meshes 

                                        Figure 1. Adaptive Refined Meshes                                                                            Figure 2. Errors on Adaptive and Uniform Meshes

[4] Fei Wang, Weimin Han, Joseph Eichholz and Xiaoliang Cheng, A Posteriori Error Estimates of Discontinuous Galerkin Methods for Obstacle Problems, Nonlinear Analysis: Real World Applications, 22 (2015), 664-679.       

[5] Fei Wang and Weimin Han, Another View for a Posteriori Error Estimates for Variational Inequalities of the Second Kind, Applied Numerical Mathematics, 72 (2013), 225-233.

 

C0 DG Methods for 4th-order Variational Inequalities

 

To solve 4th order elliptic PDEs, conforming finite element (FE) method uses C1 finite elements, which are not easy to construct and implement. To resolve this problem, nonconforming FE method have been developed. However, the nonconforming FE space needs to be carefully chosen so that the inconsistent error can be controlled. Instead, we can consider C0 DG methods to solve 4th order PDEs. The FE spaces belong to C0, instead of C1, and at the meantime, penalty terms for derivative between element boundary are added to force the derivative almost continuous. Therefore, C0 DG schemes have good accuracy with less number of freedom, so a lot of time  can be saved in solving the discretized problems. We study C0 DG methods to solve elliptic variational inequalities of 4th-order for the Kirchhoff plates. It is difficult to construct stable DG methods for such problems because of the higher order and the inequality form. For the frictional contact Kirchhoff plates, we proved that the quadratic C0 DG schemes achieve the optimal convergence order ([6]).

 

[6] Fei Wang, Tianyi Zhang and Weimin Han, C0 Discontinuous Galerkin Methods for a Plate Contact Problem, Journal of Computational Mathematics, 37 (2019), 184-200.

Interface Coupled Multi-Physics Problems

Many problems in physics and engineering contain a certain level of coupling between different physical systems, for example, fluid-structure Interaction (FSI) problems, and multi-phase flows, etc. FSI is a coupled partial differential equation system, which describes how a moving solid object interacts with the fluid surrounding it. This problem is very complex and challenging due to its highly nonlinear and coupled nature. Moreover, the position and the shape of the interface between fluid and structure is time dependent and is one of the unknowns, which greatly increases the nonlinearity of the problems both theoretically and computationally.  FSI has a wide range of applications in many areas including hydro turbines and aircraft designing, artificial heart simulations and etc. Mathematically, such a problem contains an interface where the coupling takes place. Therefore, the numerical discretization of the interface problem is very important in the applied sciences and mathematics. The standard finite element cannot achieve the optimal convergence order due to lack of resolution for the interface. The interface-fitted mesh can be used to overcome this difficulty, but if the problem is time-dependent, the domain needs to be re-meshed at each time step, which introduces interpolation error between two meshes. The extended finite element method extends the classical finite element method by enriching the solution space locally around the interface with discontinuous functions, and it is realized through the partition of unity concept. This approach provides accurate approximation for the problems with jumps, singularities, and other locally nonsmooth features within elements. The hardest part of error analysis for XFEM is the trace and inverse inequalities on the curved sub-elements divided by interface from a triangle element, especially they do not hold true for the shape irregular sub-element. Therefore, the standard analysis for finite element methods cannot be applied to the analysis of stability for the high order XFEM. Worked with Dr. Shuo Zhang (Chinese Academy of Sciences), we applied quadratic XFEM with Nitsche scheme to solve elliptic interface problems. We have proved one key inequality for any shape of interface under certain assumptions, and then we are able to show that this method achieves the optimal convergence order ([7]). Furthermore, recently, I have been working with Prof. Xu and Dr. Yuanming Xiao (Nanjing University) on arbitrary order XFEM with Discontinuous Galerkin schemes on interface problem. Optimal error estimates in the piecewise H1-norm and in the L2-norm are rigorously proved for both schemes. In particular, we have devised a new parameter-friendly DG-XFEM method, which means that no “sufficiently large” parameters are needed to ensure the optimal convergence of the scheme ([8]). This parameter-friendly DG-XFEM method can be applied to solve interface couplied multiphysics problems, like the simulations of hydroelectric power generator, cardiovascular system and hydraulic fracturing. 

 

    

 

[7] Fei Wang and Shuo Zhang, Optimal Quadratic Nitsche Extended Finite Element Method for Solving Interface Problem, Journal of Computational Mathematics, 36 (2018), 693-717.

 

[8] Fei Wang, Yuanming Xiao and Jinchao Xu, High-Order Extended Finite Element Methods for Solving Interface Problems, submitted.

Unified Framework of Finite Element Methods

With Prof. Xu, Dr. Wu, Dr. Hong, we present a unified framework ([9]) for the design of finite element methods (FEM) of different kinds, including conforming and nonconforming FEMs, mixed FEMs, hybrid FEMs, discontinuous Galerkin (DG) methods, hybrid DG methods and weak Galerkin methods.  We illustrate the main idea using a model second order elliptic boundary problem. This problem admits two main variational formulations, namely the primal and mixed formulation respectively.  The primal formulation requires certain continuity for the primal variable u, namely u belongs to H1$, while the mixed formulation requires certain continuity for the (mixed) flux variable p, namely p belongs to H(div). The design of finite element methods then amounts to an appropriate approximation of the aforementioned continuity requirements for either u or p.  There are roughly four different ways to approximately impose these continuity requirements: (1) strongly (conforming); (2) weakly (nonconforming); (3) by Lagrangian multiplier (hybrid or stabilized hybrid), and (4) by penalization (discontinuous Galerkin).  Using the notation of the DG-gradient and DG-divergence (which are reduced to standard weak derivatives when the underlying finite element spaces are conforming), every existing finite element method considered in this paper can be expressed in terms of one of the following: (1) DG-gradient and DG-gradient* (primal), (2) DG-divergence and DG-divergence* (mixed), and (3) DG-divergence* and DG-gradient* (DG). 

 

 

In light of this general framework, a new mixed DG method is proposed, and we apply it to solve linear elasticity problem with arbitrary order discontinuous finite element spaces. For the mixed methods for linear elasticity problem, it is very challenging to develop the stable mixed finite element methods because the stress tensor needs to be symmetric according to the principle of conservation of angular momentum. In [10], we study the mixed LDG method for solving linear elasticity by discontinuous Pk+1-Pk finite element pairs for the stress and displacement with k ≥ 0 for any spatial dimension in a unified fashion. We note that the stress is discretized in the DG space with strongly imposed symmetry. Our contributions are twofold. First, by introducing a mesh dependent norm for the stress, we give a prior error analysis, which shows that optimal L2-error estimate for displacement and optimal Hh(div) error estimate for stress. Second, when the Pk+2−Pk+1 Stokes pair is stable and k ≥ d, we prove the optimal L2-error estimate for the stress by the BDM projection and a symmetrization technique.

 

[9] Qingguo Hong, Fei Wang, Shuonan Wu and Jinchao Xu*, A Unified Study of Continuous and Discontinuous Galerkin Methods, SCIENCE CHINA Mathematics, 62 (2019), 1-32.

 

[10] Fei Wang, Shuonan Wu and Jinchao Xu, A Mixed Discontinuous Galerkin Method for Linear Elasticity with Strongly Imposed Symmetry, Journal of Scientific Computing, 82:2 (2020).

 

[11] Yanxia Qian, Shuonan Wu and Fei Wang, A Mixed Discontinuous Galerkin Method with Symmetric Stress for Brinkman Problem Based on the Velocity-Pseudostress Formulation, Computer Methods in Applied Mechanics and Engineering, 368 (2020), 113177.

Virtual Element Methods for VIs and Hemivariational inequalities

The Finite element method (FEM) is a natural numerical discretization approach for variational inequalities. The classical FEM works on the elements with simple geometries, like triangles and rectangles. Due to the flexibility on constructing the local function space, the discontinuous Galerkin (DG) method can handle very general meshes with hanging nodes, which make them very suitable for hp-adaptivity. However, the DG method needs large number of degrees of freedom. Recently, borrowing the ideas from the mimetic finite difference method, the virtual element method  (VEM), which can be regarded as a generalization of the classic FEM to general polygonal meshes, have been developed for solving a variety of partial differential equation. The virtual element method can handle very general (non-convex) polygonal elements with an arbitrary number of edges. In addition, it allows geometrical hanging nodes in the meshes, even they are treated as vertices of the polygonal elements in practice, so it is easy to implement h-adaptive strategy for the VEM. We study the virtual element method for solving obstacle problem [10], simplified friction problem [11], and plate frictional contact problem [12]. The optimal error estimates are established for the lowest-order virtual element methods, and numerical examples are given to support the theoretical results.  

 
      
 
[10] Fei Wang and Huayi Wei, Virtual Element Methods for Obstacle Problem,  IMA Journal of Numerical Analysis, 40 (2020), 708–728, (published online 2018).
 

[11] Fei Wang* and Huayi Wei, Virtual Element Method for Simplified Friction Problem, Applied Mathematics Letters, (2018) https://doi.org/10.1016/j.aml.2018.06.002.

 

[12] Fei Wang and Jikun Zhao, Conforming and Nonconforming Virtual Element Methods for a Kirchhoff Plate Contact Problem, IMA Journal of Numerical Analysis 41 (2021) , 1496–1521.

[13] Yanling Deng, Fei Wang* and Huayi Wei, A Posteriori Error Estimates of Virtual Element Method for a Simplified Friction Problem, Journal of Scientific Computing, 83:52 (2020), DOI: 10.1007/s10915-020-01242-9. 

[14] Min Ling, Fei Wang* and Weimin Han, The Nonconforming Virtual Element Method for a Stationary Stokes Hemivariational Inequality with Slip Boundary Condition, Journal of Scientific Computing, (2020) 85:56，https://doi.org/10.1007/s10915-020-01333-7. 

[15] Fei Wang*, Bangmin Wu and Weimin Han, The Virtual Element Method for General Elliptic Hemivariational Inequalities, Journal of Computational and Applied Mathematics, 389 (2021) 113330.