1. 表面活性剂
素有“工业味精”之称的表面活性剂广泛应用于微液滴流动控制、石油工业、环境工程和食品加工等领域,是最重要的工业助剂之一。它的少量添加即可显著地改善液体界面的化学性质和表面张力特性。进而改进生产工艺、降低消耗和提高产品质量。含表面活性剂的界面行为的数值模拟是一项极具挑战的工作。我们采用耦合的LBM方法与有限差分法,发展了针对含表面活性剂的液滴运动求解的高性能程序。以下是不含表面活性剂和含表面活性剂的液滴在剪切流动中的运动情况对比:


(a) (b)
图1 剪切流动下二维双液滴的碰撞。模拟参数为Ca_e=0.1,Re=0.4
(a)不含表面活性剂时,两个液滴合并成一个大液滴,(b)含表面活性剂时,两个液滴互相滑过,不发生合并

图2 剪切流动下三维液滴的破裂过程,含表面活性剂时,液滴断裂为三个子液滴
液滴在固体壁面的运动、变形和破裂现象广泛存在于石油、化工和环境领域,如土壤地下水修复、提高油气采收率和二氧化碳地质封存等。在上述过程中,添加表面活性剂会显著地减小两流体间的界面张力和改变壁面润湿属性,导致含表面活性剂液滴动力学行为与干净液滴存在显著差异。课题组根据杨氏方程和Langmuir状态方程建立了接触角与表面活性剂界面浓度之间的函数关系,并通过接触角几何公式实施动态接触角,在格子玻尔兹曼框架下发展了包含表面活性剂浓度影响的润湿边界条件;研究了库塔流中含表面活性剂的液滴在静止壁面上的运动、变形及破裂行为,并对比分析了表面活性剂在不同粘性比下对液滴破裂临界毛细数的影响规律,如下图所示。

图3 不同粘性比下干净液滴的破裂临界毛细数
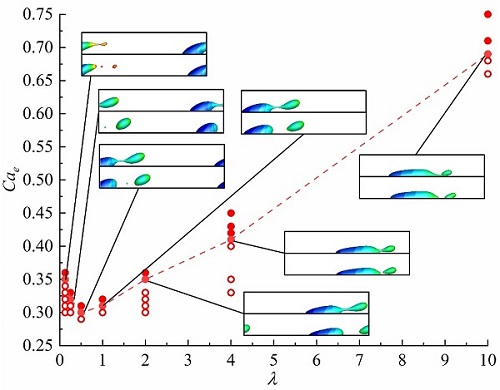
图4 不同粘性比下含表面活性剂液滴的破裂临界毛细数
在液滴生成实验中,通常会添加过量的表面活性剂(远高于临界胶束浓度)到微流体系统,导致由表面活性剂在界面非均匀分布产生的马兰戈尼应力完全被抑制。此外,表面活性剂往往具有毒性,过量添加表面活性剂不仅对人体健康产生不利影响,而且会产生巨大的分离成本。为选择合理的表面活性剂浓度,本课题组发展了含可溶表面活性剂的两相流动计算方法,研究了表面活性剂浓度对微通道中液滴生成模式、生成液滴尺寸、通道上游压力以及主通道压力变化的影响规律。以下是不同表面活性剂浓度下液滴生成情况对比:



图5 不同表面活性剂浓度下液滴生成过程。从(a)至(b)表面活性剂浓度分别为psi=0,0.35和0.4。其它参数取为:毛细数Ca=0.0125和流量比Q=0.2
2. 非牛顿流
简单剪切流动中的液滴变形与破裂行为在微流控技术、乳化混合和提高原油采收率等工业过程中广泛存在。影响该液滴动力学行为的主要因素有:通道的几何结构及属性、运行参数和流变属性。在流变属性方面,非牛顿流变性质会显著改变流体粘度等特性,但以往研究工作多关注于牛顿流体,非牛顿流变性质影响下的液滴变形与破裂机制仍有待探索。课题组采用LBM方法对该流动现象进行数值研究,下图显示了非牛顿流变特性对液滴破裂行为的影响。

(a)

(b)
图6 简单剪切流动下(壁面限制比0.7,毛细数0.4,雷诺数0.1),牛顿(a)和非牛顿(b)负载流体中牛顿液滴的演化过程
液滴或负载流体的非牛顿流变性质是影响液滴行为的重要因素,不仅涉及流体粘度剪切稀释、增稠等变化,而且粘弹性非牛顿流体会通过粘弹性力的作用影响液滴行为。课题组最近发展并应用LBM两相流动计算方法,研究并获得了Giesekus粘弹性负载流体中浸没液滴的剪切变形和破裂规律,以及Oldroyd-B粘弹性流变性质影响下壁面附着液滴的变形规律和受力机制。下图展示了壁面液滴运动,界面上受到的粘性力和弹性力分布的对比图。
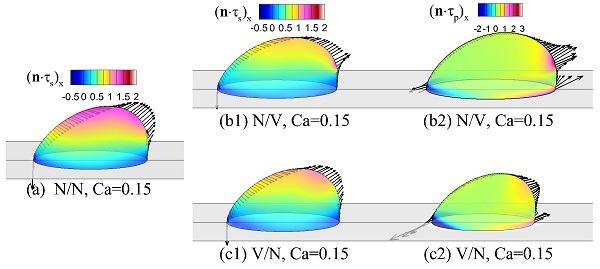
图7 壁面液滴运动界面受力分布对比,其中N/N表示牛顿流体系统;N/V表示牛顿液滴/粘弹性负载流体系统;V/N表示粘弹性液滴/牛顿负载流体系统。
3. 复合液滴


图9 复合液滴在振荡剪切流中的变形过程

图10 复合液滴在振荡剪切流中的破裂过程
4. 多孔介质多相流
多孔介质多相流在工业领域有很多应用,例如石油开采,CO2封存以及燃料电池内的水管理等。由于多孔介质内的多相流动受到重力、毛细力、粘性力以及孔隙结构等多方面的影响,完全理解多孔介质内的多相流是一项极具挑战力的工作。我们基于LBM方法中的颜色模型发展了针对多孔介质内部油水两相流、油水气三相流的高性能计算程序,并对其内部流动进行了精细的刻画。下图为不同类型多孔介质内的两相、三相渗流模拟结果:


图11 毛细数为5*10-5的两相drainage和imbibition过程

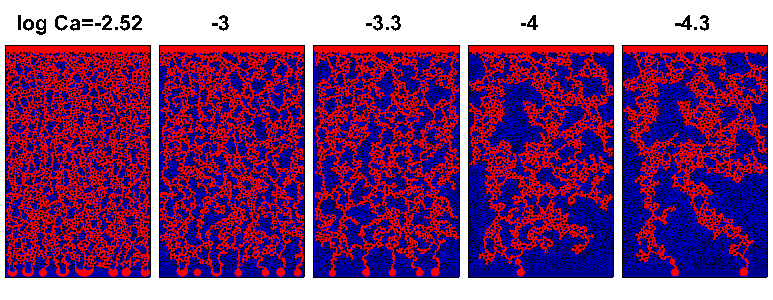
图12 在各向同性与各向异性多孔介质内不同毛细数下两相drainage过程稳定时的相分布

图 13 不同润湿性条件下Berea砂岩内的三相渗流。其中,多孔介质模型由真实的Berea砂岩切片提取而来。
自发吸入(自吸)是指润湿流体在毛细力的作用下自发侵入微小流道,是多孔介质渗流过程中的一种重要现象。开展孔隙尺度自吸过程数值模拟的难点主要包括两个方面:(1)深度方向的三维效应在促进驱替流体突破毛细阀压力时的作用不可忽略;(2)为确保界面曲率捕捉的准确性,通常需要在深度方向布置足够多的网格,从而导致高昂的计算成本。到目前为止,仍没有较好地复现实验中自吸现象的数值模拟结果见诸报道。鉴于此,课题组发展了一种既能考虑三维效应,又远小于三维计算量需求的准三维数值模型。随后应用该模型对多孔介质微模型内的自吸驱替过程开展了数值研究。同时,在理论层面上,我们修正了经典Lucas-Washburn公式,对稳定驱替过程中饱和度与时间之间的关系进行了精准预测。下图展示了无水乙醇自吸侵入多孔介质微模型过程的准三维数值模拟、实验和理论预测三者结果对比。

图14 无水乙醇自吸侵入多孔介质微模型实验与数值模拟过程
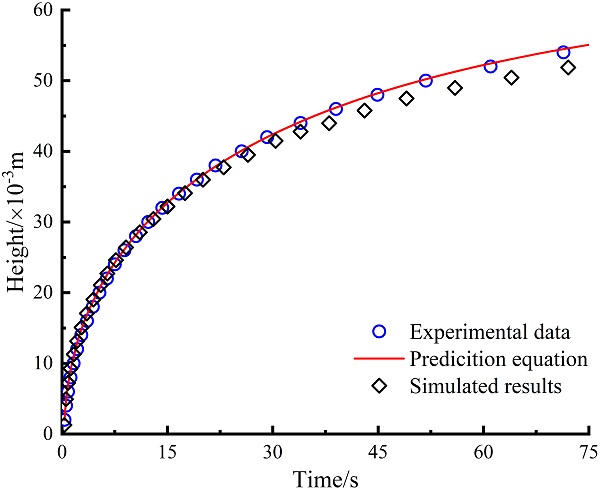
图15 无水乙醇自吸侵入多孔介质微模型过程的准三维数值模拟、实验和理论预测三者结果对比
5. 液滴微流控
双乳剂是指water in oil in water(水包油包水)等液滴内含有液滴的乳剂。基于双乳剂外层流体对内层流体的包裹结构,可以防止内部活性物质的降解;通过调节外层流体的属性,实现对内部流体的可控释放;以及提供微化学反应环境等。因此,双乳剂在制药、化工、材料、食品加工和个护等行业取得了广泛应用。然而,双乳剂制备过程中涉及复杂的三相流体动力学行为,对乳剂生成机理的认识提出了很大的挑战。课题组采用三相LBM方法复现了双乳剂制备过程中的单步和双步制备行为(下图所示),并进一步研究了各相关参数的影响。

图16 双交叉型通道内双乳剂液滴的单步生成

图17 双交叉型通道内双乳剂液滴的双步生成
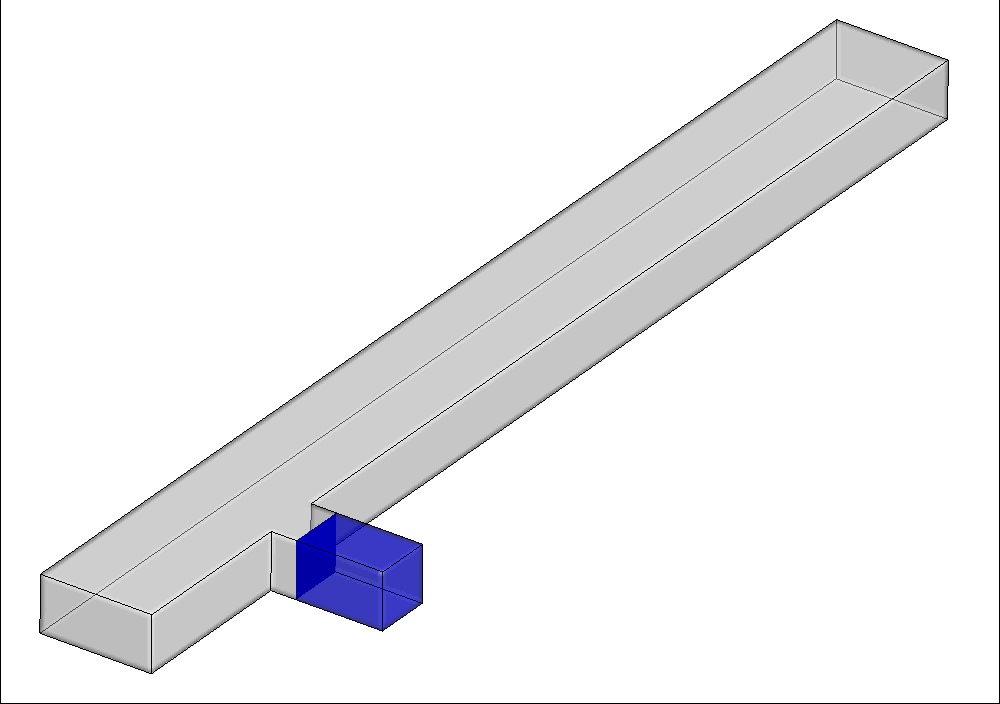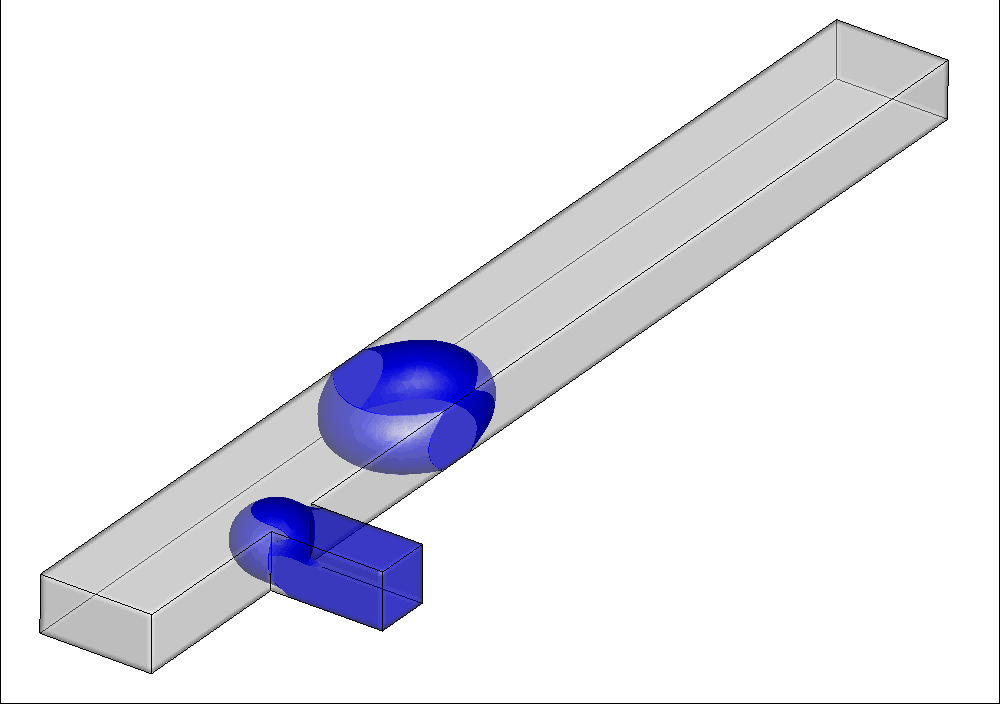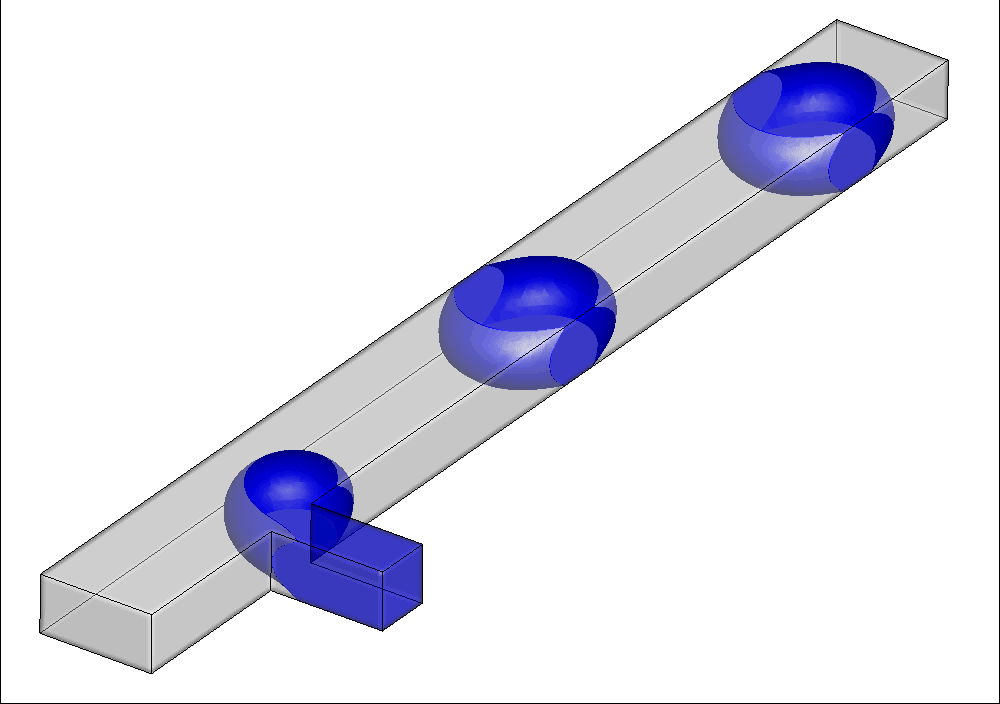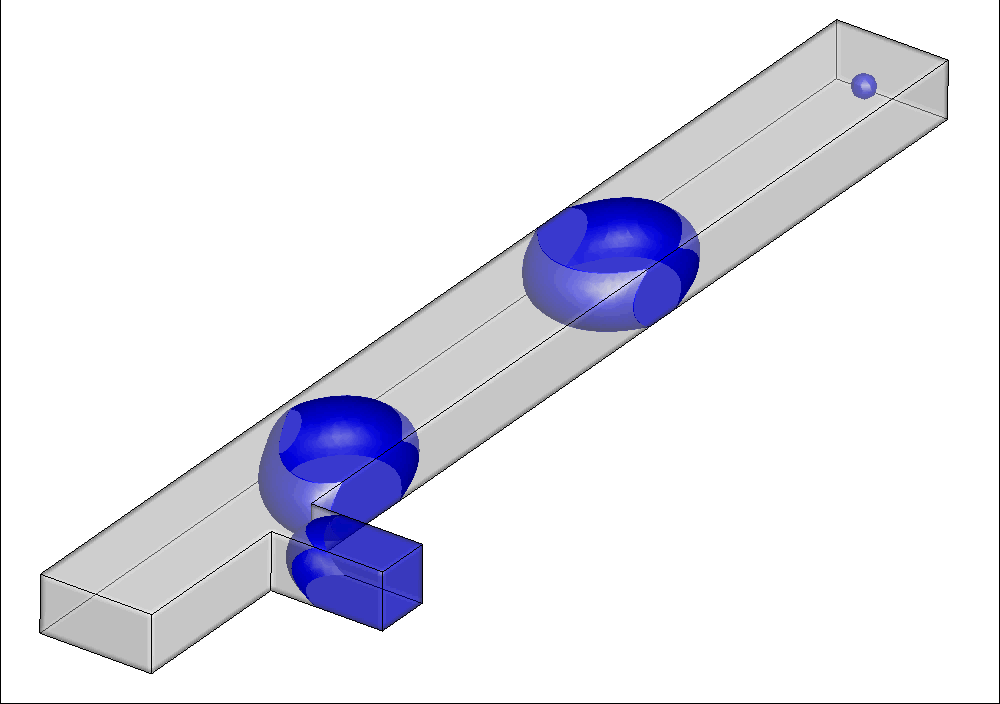

图18 T型微通道内的液滴生成 图19 激光诱导的液滴热毛细运动
6. 气-液-固三相流
气-液-固三相流普遍存在于自然界和工业过程中,如打水漂、轮船兴波、喷墨打印以及矿物浮选等。在小尺度气-液-固三相流动问题中,表面张力、固体表面润湿性、固体受到来自气-液界面的毛细力通常起主导作用。目前,毛细力的准确计算以及处理气-液两相较大的密度差异仍然面临挑战。为此,课题组提出了一种适用于曲线固体边界的毛细力计算模型,并基于格子Boltzmann相场方法发展了一套可用于模拟大密度比气-液-固三相流动问题的数值方法。该数值方法可以较好地复现理论预测和试验结果(图20)。利用该方法研究了气-液界面上三个圆形颗粒在表面张力作用下的自组装过程(图21)。

图20. 颗粒入水不同时刻模拟结果(右侧)与试验结果(左侧)的对照

图21. 颗粒在气-液界面上的自组装
胶体颗粒具有稳定液-液界面的作用,在乳液制备中得到了广泛的应用,但其确切的作用和潜在的影响机制尚不清楚。课题组基于三维格子玻尔兹曼颜色梯度两相流模型,采用新的毛细力模型和求解粒子动力学的动量交换法,研究了表面嵌有固体颗粒的液柱的Rayleigh−Plateau不稳定性行为 (图22动画)。研究发现,增大颗粒浓度可以增强液柱的稳定性,从而延缓破裂(图23)。在固体颗粒轻度疏水条件下液柱最稳定,对应的初始气-液界面自由能最低。由于液柱内外不同的压力梯度以及固体颗粒受到的背向颈部的毛细力,疏水颗粒倾向于在变形液柱颈部附近较为松散地聚集,而亲水颗粒则远离颈部密集地聚集(图24)。对于疏水颗粒,除了初始气-液界面自由能的影响外,与液体流动方向相反的颗粒自组装也有助于延迟液柱的破裂。

图22 表面带有颗粒的液柱的Rayleigh−Plateau不稳定性过程

图23 在干净(左列)和有颗粒(右列)两种情况下,(a)短、(b)长液柱的破碎过程

图24 (a)亲水颗粒,(b)疏水颗粒在变形液柱上的分布
7.相变
物质在一定温度和压强下稳定相态一般为三种,即固相,液相和气相,不同相态之间的相互转变称为相变。相变现象广泛存在于自然界,日常生活以及工业生产实践中,如冬季水面结冰,烧水时的沸腾,芯片液冷却蒸发等。尽管相变现象普遍有趣,但因其过程极其复杂,既涉及各种物理组分之间的相互联系,又包含流动、潜热传递以及相界面的出现、变形和消失等,目前对相变的机理仍不清楚,且无普适有效的模拟手段。课题组基于前人的混合热LB模型,模拟了平面上的液体沸腾过程,再现了池沸腾的三个经典阶段(如下图),同时还模拟了具有不同接触角的曲面上液体膜态沸腾的发展过程(如下图)。

(a)核态沸腾阶段

(b)过渡沸腾阶段

(c) 膜态沸腾阶段
图25 平面上液体的沸腾过程



(a)曲面接触角为60° (b)曲面接触角为90° (c) 曲面接触角为120°
图26 不同接触角的曲面上液体膜态沸腾的发展过程




