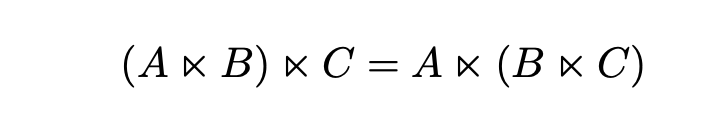数学与统计学院 应用数学系
教授、博导
西安交通大学青年拔尖人才计划 (A类) (2025)

数学与统计学院 应用数学系
教授、博导
西安交通大学青年拔尖人才计划 (A类) (2025)
Email: kuize.zhang@xjtu.edu.cn
拟招收硕士研究生和博士研究生,欢迎对理论计算机科学和控制论感兴趣的同学把简历等相关内容发送到以上邮箱。




工作经历:
|
2025.03至今 |
西安交通大学,数学与统计学院,教授 |
| 2024.11-2025.01 | 中国科学院数学与系统科学研究院,访问学者 |
|
2024.05-2024.10 |
意大利卡利亚里大学,访问教授 |
|
2022.04-2024.03 |
英国萨里大学,讲师 |
|
2020.07-2022.04 |
德国柏林工业大学,洪堡学者(博士后) |
|
2017.09-2020.04 |
瑞典皇家理工学院,博士后 |
|
2016.09-2017.08 |
德国慕尼黑工业大学,博士后 |
学习经历:
| 2009.09-2014.12 | 哈尔滨工程大学,自动化学院,博士 |
| 2005.09-2009.06 | 哈尔滨工程大学,理学院,学士 |
离散状态动态系统的形式化验证
相关领域:控制论,理论计算机科学、信息物理系统等
研究的模型包括:布尔控制网络、有限自动机、Petri网、幺半群上的加权有限自动机、定时自动机、实时自动机等
探索离散状态动态系统中可判定的性质的简洁、普适、高效的检验与强化方法,及其潜在的应用
主要成果为相应研究领域(布尔控制网络、离散事件系统)教科书内容
代表性结果包括:
提出布尔控制网络的能观性图,并结合有限自动机理论,给出布尔控制网络四种能观性的检验方法。相关讲义见https://link.springer.com/article/10.1007/s11768-022-00122-x,简要课程视频见https://m-stp.lcu.edu.cn/xzyd/xzzm/565246.htm。
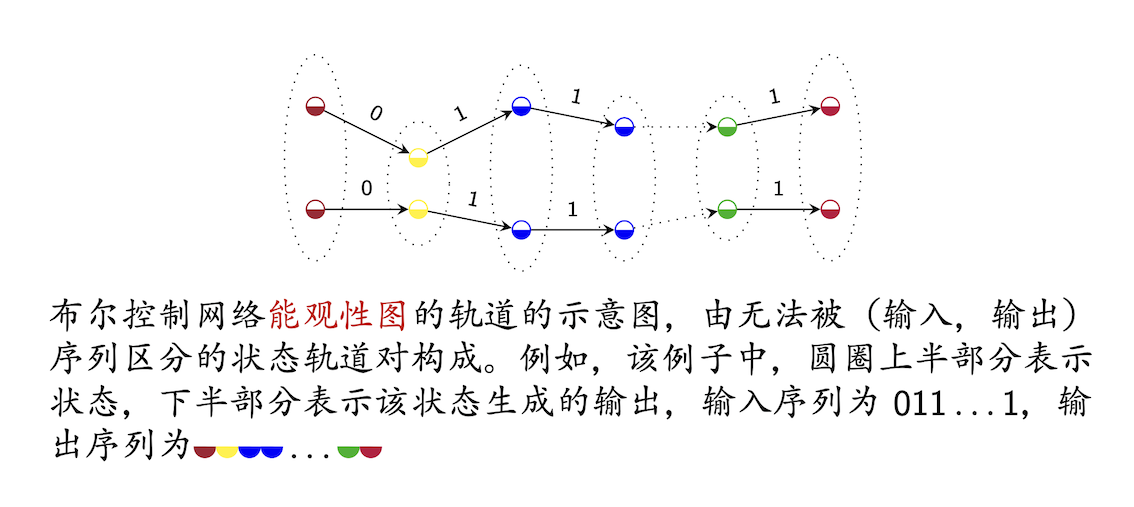
能观性图及其邻接矩阵(被同行称为能观性矩阵或者并行扩展)的基本想法已经被同行学者广泛使用并推广,解决大量相关问题,如布尔控制网络的可重构性检验、集可达性检验,布尔网络的能观性扰动分析、极小能观性分析,奇异布尔控制网络的能观性检验,概率布尔网络的能观性检验、极小能观性分析,标签随机图的能观性及可重构性检验,马尔可夫跳变布尔网络的极小有限时间能观性分析。
能观性图或者能观性矩阵方法被很多学者使用并发展:
[1] K. Zhang, L. Zhang, and R. Su. A weighted pair graph representation for reconstructibility of Boolean control networks. SIAM Journal on Control and Optimization, 54(6):30400-3060, 2016.
[2] D. Cheng, H. Qi, T. Liu, and Y. Wang. A note on observability of Boolean control networks. Systems & Control Letters, 87:76-82, 2016.
[3] Q. Zhu, Y. Liu, J. Lu, and J. Cao. Observability of Boolean control networks. Science China Information Sciences, 61(9):092201, 2018.
[4] Y. Guo. Observability of Boolean control networks using parallel extension and set reachability. IEEE Transactions on Neural Networks and Learning Systems, 29(12):6402-6408, 2018.
[5] S. Zhu, J. Cao, L. Lin, L. Rutkowski, J. Lu, and G. Lu. Observability and detectability of stochastic labeled graphs. IEEE Transactions on Automatic Control, 68(12):7299-7311, 2023.
[6] L. Lin and J. Lam. Observability categorization for Boolean control networks. Network Science and Engineering, pages 1-12, 2023.
[7] L. Wang, Z. Xia, Y. Liu, S. Azuma, and W. Gui. Minimal finite-time observability of Markovian jump Boolean networks. Systems & Control Letters, 196:106007(1-9), 2025.
[8] Y. Yu, M. Meng, J. Feng, and G. Chen. Observability criteria for Boolean networks. IEEE Transactions on Automatic Control, 67(11):6248-6254, 2022.
[9] S. Zhu, Y. Jia, and J. Feng. Observability of probabilistic Boolean networks via matrix approach. IEEE Transactions on Control of Network Systems, 10(2):834-840, 2023.
[10] Y. Li, H. Li, and G. Xiao. Observability verification system analysis for observability and reconstructibility of probabilistic logical control networks. IEEE Transactions on Circuits and Systems I: Regular Papers, 72(8):4273-4283, 2025.
[11] Y. Liu, J. Zhong, D.W.C. Ho, and W. Gui. Minimal observability of Boolean networks. Science China Information Sciences, 65(5):152203(1-12), 2022.
[12] L. Wang, Z. Xia, Y. Liu, S. Azuma, and W. Gui. Minimal finite-time observability of Markovian jump Boolean networks. Systems & Control Letters, 196:106007(1-9), 2025.
[13] S. Wang and H. Li. Graph-based function perturbation analysis for observability of multivalued logical networks. IEEE Transactions on Neural Networks and Learning Systems, 32(11):48390-4848, 2021.
[14] T. Li, J. Feng, and B. Wang. Reconstructibility of singular Boolean control networks via automata approach. Neurocomputing, 416:19-27, 2020.
离散事件系统中,提出并发合成算子,并基于该算子提出离散事件系统用于检验和强化基本性质的新理论框架。新理论框架带给离散事件系统领域的本质性改变包括:
在有限自动机中,给出统一的检验基于推断的性质和基于隐藏的性质的方法。在检验基于推断的性质(如强可检测性、可诊断性、可预测性)方面,去掉被广泛使用接近30年的无死锁和无不可观的环两个基本假设。在检验基于隐藏的性质方面,与经典的观测器(即,由Rabin和Scott于1959年提出的不确定性有限自动机的幂集构造)相结合,给出检验各种不透明性统一的且是当前最高效的方法。
在性质强化方面,与引领该领域过去30多年发展的Ramadge-Wonham监督控制理论框架(1987)相比,新理论框架有两个显著优点:
新理论框架的实现效率更高。监督控制理论框架在有限自动机中的实现问题为EXPTIME-完全,所以无法在多项式时间内实现;而新理论框架可以在多项式时间内加强一个性质,如果该性质可以在多项式时间内得到检验。
新理论框架可以在显著更多的系统中实现。监督控制理论框架可以在满足无死锁和无不可观的环两个基本假设的有限自动机中完全实现,而新理论框架不仅可以在全部的有限自动机中实现,还可以在无穷状态系统中强化可判定的性质。

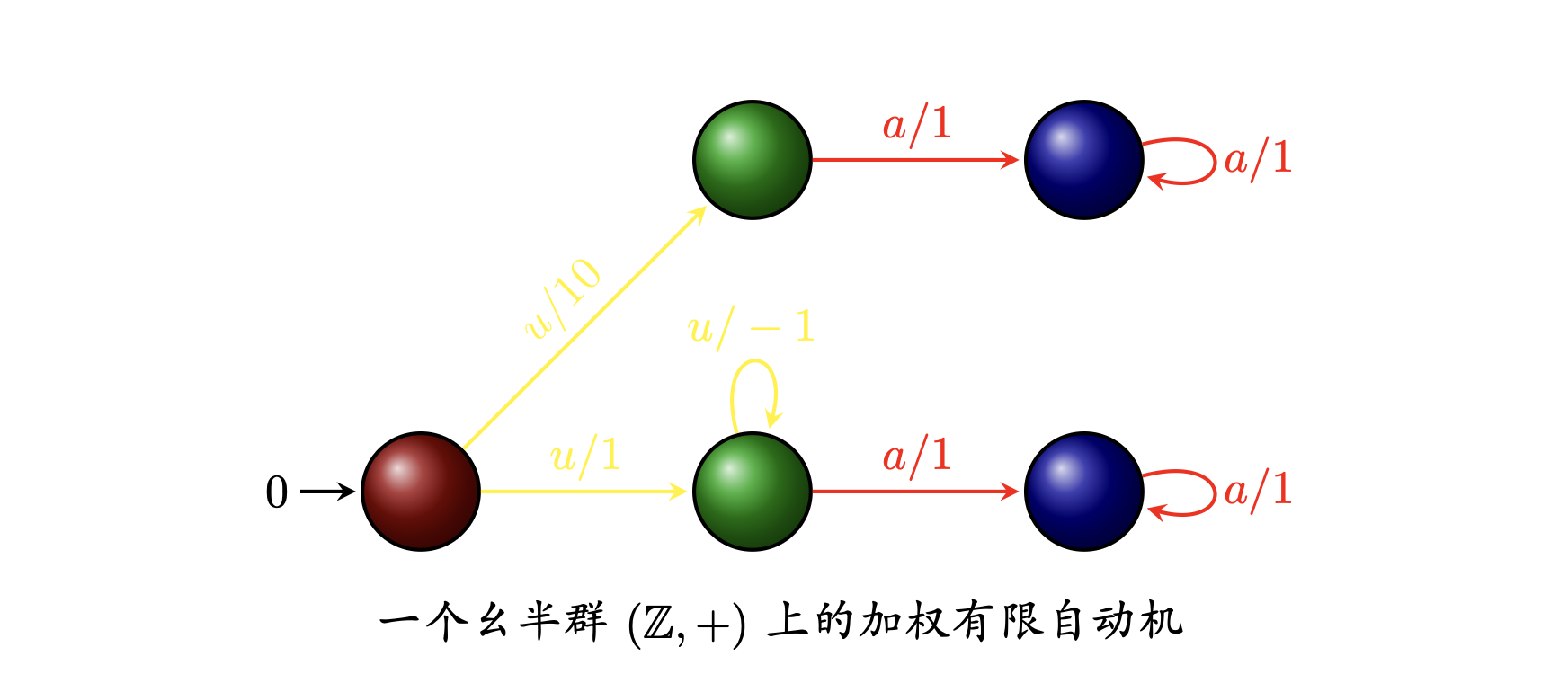
提出幺半群上的加权有限自动机,并提出基本工具——并发合成算子和观测器。基于这两个基本工具,可以探索对这类新自动机中各种性质及其潜在应用领域的研究。
证明矩阵左半张量积一般形式的结合律。给出向量商空间(可数无穷维)的一个基底。